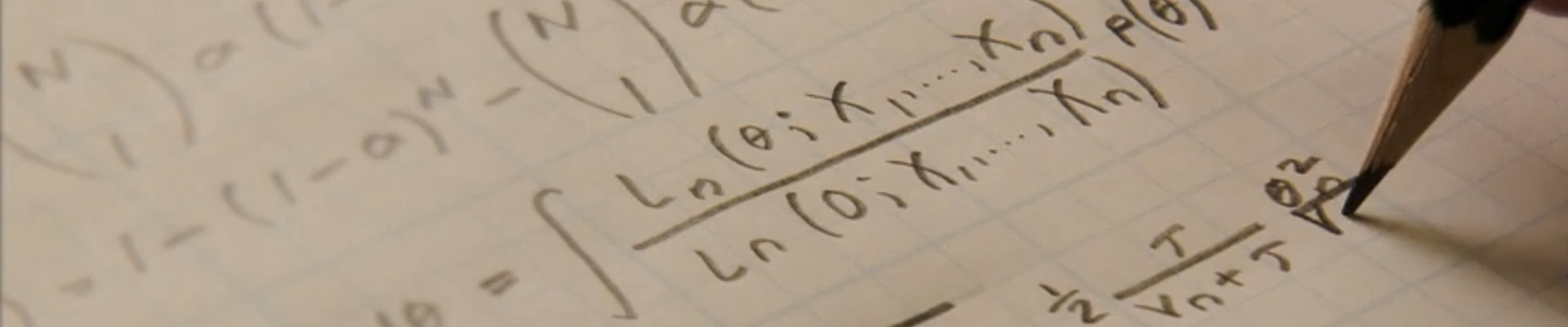Area Under the Curve

1. Confusion Matrix

Here a typical Confusion matrix after a test with a binary classification problem.

	Ground Truth
		Positive	Negative
Predicted	Positive	TP	FP
	Negative	FN	TN

The distribution of the classes might look something like this:

The x-axis is the predicted probability and the y-axis is the count or frequency of observation. For example, at prob=0.2, the number of observations is 2. The green line shows the threshold used to separate the positive and negative labels for this test.

2. Definitions

2.1 Recall/Sensitivity

Recall/Sensitivity is a measure of the probability that the estimate is Positive given all the samples whose True label is Positive. In short, how many positive samples have been ientified as positive. It is also called the True Positive Rate.

$$sensitivity = recall = \frac{TP}{TP + FN}$$

	Ground Truth
		Positive	Negative
Predicted	Positive	TP	FP
	Negative	FN	TN

2.2 Precision

Precision is defined as the number of TP over the number of all samples predicted to be positive:

$$P = \frac{TP}{TP + FP}$$

	Ground Truth
		Positive	Negative
Predicted	Positive	TP	FP
	Negative	FN	TN

2.3 Specificity:

Specificity, also known as True Negative Rate, is not precision.

$$S = \frac{TN}{TN + FP}$$

	Ground Truth
		Positive	Negative
Predicted	Positive	TP	FP
	Negative	FN	TN

3. Metrics to evaluate classification test/model:

3.1 F score

The F-score is defined as:

$$F_{\beta} = \frac{(1 + \beta^2) (P + R)}{\beta^2 P + R}$$

where $P$ is the Precision, $R$ is the Recall and $\beta$ takes the common values $\beta=0.5, 1, 2$.

3.2 Precision/Recall curve

The Precision/Recall curve shows the Recall (in y-axis) and Precision (x-axis) for various threshold values / decision boundary. The ideal point is Precision=1 and Recall=1.

3.3 ROC (Receiver Operating Characteristic) Metric

ROC is a visual way of inspecting the performance of a binary classification algorithm. ROC curve is the plot of TPR versus FPR (1-specificity) for different threshold values.

$$\begin{align} 1 - Spec = 1 - \frac{TN}{TN + FP} = \frac{TN + FP - TN}{TN + FP} = \frac{FP}{TN + FP} \end{align}$$

Below is a typical ROC curve for 2 tests where each data point is the sesitivity and specificity when uisng a particular threshold.

Let’s look at several ROC curve shape and what it tells us about the performance of the classifier. The baseline indicates that the classifier is not better than making random guess. The Underperforming model would have data points below the baseline. A good classifier will points above the baseline.

3.3 AUROC: Area under ROC

AUC is useful when comparing different model/tests, as we can select the model with the highest AUC value.

$$\begin{align} AUC &= 0 \rightarrow \text{ bad } \\ AUC &< 0.5 \rightarrow \text{worst than random guessing } \\ AUC &= 0.5-0.6 \rightarrow \text{same as random guessing } \\ AUC &= 0.6-0.7 \rightarrow \text{Poor } \\ AUC &= 0.7-0.8 \rightarrow \text{Fair } \\ AUC &= 0.8-0.9 \rightarrow \text{Good } \\ AUC &= 0.9-1.0 \rightarrow \text{Excellent } \end{align}$$

AUROC can be calculated using the trapezoid rule: adding the area from the rapezoids:

4. Some Notes

4.1 Imbalanced dataset

Most problems do not deal with balanced class and ROC becomes less powerful when using imbalanced datasets.

The distribution of the classes might look something like this:

One effective approach to avoid potential issues wit himbalanced datasets is using the early retrival area, where the model performance can be analyze with fewer false positive or small FPR.

4.2 Probability calibration

ROC and AUROC are insensitive to whether the predicted probabilities are properly calibrated to actually represent probabilities of class membership.

4.3 Multi-class problems

ROC curves can be extended to problems with 3 or more classes.

4.4 Choosing Threshold

Choosing a classification threshold is a business decision: minimize FPR or maximize TPR.

5. Precision/Recall Curve

PR is more appropriate if the data class distribution is highly skewed class imbalance.