The goal of a Sorting Algorithm is to change the order of the elements in an array. The sorting can be done either in-place, re-order the datastructure within, or not-in-place by copying to a new datastructure. The in-place algorithms are low space complexity. The choice of an algorithm for an application is mainly driven by the application itself.
This is the last part of a series of 3 short posts on the topic of Sorting Algorithms:
- Bubble Sort
- Merge Sort
- Quick sort
Part III: Quick Sort
The algorithm of quick sort goes as follow: given an array,
-
pick a value at random. This is called the pivot.
-
Move all values larger than pivot above it and,
-
Move all values lower than pivot below it.
-
Reiterate for all elements
The convention is to pick the pivot as the last element:
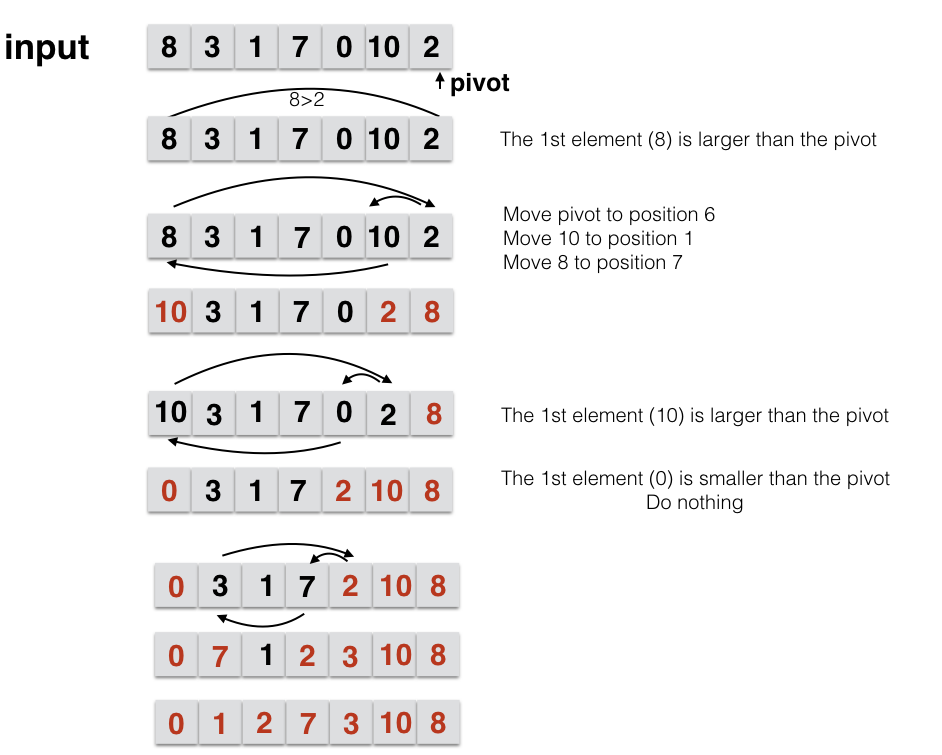
After all the iterations with the current pivot (=2) are completed, we know that all elements that are below or above are less or greater than 2, so 2 is in the right place.
Now we split the problem in two parts: above the pivot and below the pivot.
On the lower part i.e at the position (pivot - 1), we select a new pivot : that is the last element of the lower part of the array.
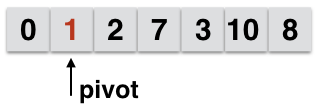
As such, the new pivot is 1, and now we iteratively compare it with all elements before it.
On the higher part, we select a new pivot 8 (the last element of the higher part)

The new pivot is 3, and we do similar comparison.
Efficiency
-
the worst case: the array is already ordered If the pivot is already in the right place, we still need to compare to all elements. Same thing is done if the 2nd pivot is also at the right place. So we end up comparing to every element except the one at the end. So in the worst case, the efficiency is O($n^2$).
-
Average and best case complexity: O(n log (n))
Tips: Never use quicksort if the array is already sorted.
Optimization tricks
-
when we split the array, we can setup the computer to sort the 2 halves at the same time: use less time and same ressources.
-
rather than selecting the last element as the pivot, select the last few elements and then the median as the pivot.
The space complexity of quicksort is constant.
Pseudo-code implementation
- Condition:
1
2
3
4
5
a[j] > a[p]
increment j
a[j] <= a[p]
increment i
swap value i and j

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
partitioning (a, p, q):
i <-- p -1
pivot <-- q
for (p to q):
{
if (a[j] <= a[pivot]):
i = i + 1
swap(a[j], a[i])
}
return i #this will be q for next iteration
quicksort(a, p, q):
{
if p < r:
{
q <-- partition(a, p, r)
quicksort(a, p, q-1)
quicksort(a, q+1, r)
}
}
Another implemenation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
test = [21, 4, 3, 1, 9, 20,15, 10, 20, 25, 6, 21, 14]
def partition(a, first, ip):
print("**************************")
if ip > first:
while ip > first:
print('*** {} |ip{}, first{}'.format(a, ip, first))
if a[ip] <= a[first]:
prev = a[ip -1]
ip_val = a[ip]
first_val = a[first]
a[first], a[ip-1], a[ip] = prev, ip_val, first_val
ip = ip -1
print('*** {} |ip{}, first{}'.format(a, ip, first))
else:
first = first + 1
print('*** {} |ip{}, first{}'.format(a, ip, first))
return ip
def sorting(a, q, r):
if q < r:
ip = partition(a, q, r)
quicksort(a, q, ip-1)
quicksort(a, ip +1, r )
return a
else:
return a
def quicksort(a):
q = 0
r = len(a) - 1
return sorting(a, q, r)
print(quicksort(test, 0, len(test)-1))