This is a several part summary of the Udemy lesson: Blockchain and Bit coin fundamentals completed with my own research. Welcome to Part 3.
The focus of Part 3 is the Byzantine Fault Tolerance.
Blockchains are decentralized ledgers, which by definition are not controlled by a central authority. Due to the value stored in these ledgers, bad actors have economic incentives for instance to try and cause faults. In the absence of BFT, a peer is able to transmit and post false transactions effectively nullifying the blockchaine’s reliability. Furthermore, there is no central authorityto take over and repair the damage. The byzantine Gneeral’s Problem is a classic problem faced by any distributed computer system network.
In distributed computing there is this classic problem that is generally explains by the Byzantine generals :
We will start with the 2 general problem and generalize to several.
Intro
Intro Whenever a new transaction is broadcasted to the network, nodes have the option to include that transaction to their copy of the ledger or to ignore it. When the majority of the actors which compose the network decide on a single state, consensus is achieved.
A fundamental problem in distributed computing and multi-agent systems is to achieve overall system reliability in the presence of a number of faulty processes. This often requires processes to agree on some data value that is needed during computation. Examples of consensus include whether to commit transaction to a database, agreeing on the identity of a leader, state machine replication, and atomic broadcasts.
Real world applications include: clock synchronization, Page Rank, smart Power grids, control of UAVs (and multiple robots/agents).
The consensus problem requires agreement among a number of processes (or agents) for a single data value. Some of the process (agents) may fail or be unreliable in other ways. So consensus must be Fault Tolerant or resilient. The process must somehow put forth their candidate values, communicate with one another, and agree on a single consensus value.
One approach to generating consensus for all process (agents) to agree on a majority value. In this context, a majority requires at least one more than 1/2 of available votes: where each process is given a vote.
However, 1 or more faulty processes may skew the resultant outcome such that consensus may not be reached or reached incorrectly: for example 1 agnet or more temper with his ledger. In order to create a secure consensus protocol, it must be fault tolerant.
The 2 general problems
Principle: 2 generals are attacking a common enemy. General 1 is the leader and General 2 the follower. Each general has an army on its won: taken individuallya single army cannot defeat the enemy. Thus, they need to cooperate and attack at the same time.
In order for them to communicate, and decide on a time to attack, G1 has to send a messenger across the enemy’s camp that will deliver the time of the attack to G2. However, the messenger coudl get captured by the enemies and the msg won’t be delivered. That will result in G1 attacking while G2 holds.
Assume that the 1st message is received by G2, then now G2 needs to acknowledge (ACK) and sends a msg back to G1, thus repeating the same scenario. This extends to infinite ACK’s and thus the generals are unable to reach an agreement.
The 2 generals problem has been proven to be unsolvable
Byzantine Generals
The Byzantine Generals Problem is an extension of the 2 generals problem with more than 2 generals and where 1 or more generals are a traitor meaning they lie about their choice (agree to attack at 9AM, but then hold off). In the case of BGP, there is one general that is the commander and the other are lieutenants. In order to achieve consensus here the commander and every lietenant must agree on the same decision. Several Byzantine generals and their respective portion of the Byzantine army have surrounded a city. They must decide in unison whether or not to attack. If some generals attack without the others, their siedge will end in tragedy. The generals are usually separated by distance and have to pass msgs to communicate.
Formally put : Byzantine Generals Problem : a commanding general must send an order to his (n-1) lieutenant generals such that IC1 all loyal lieutenants obey the same order . IC2 is the commanding general is loyal , then every loyal lieutenant obeys the same order he sends. If the commander is a traitor, consensus must still be achieved.
Theorem: For any , algorithm OM() reaches consensus if there are more than 3 generals and at most traintors.
This implies that the algo can reach consensus as long as 2/3 of the actors are honest. If the traitors are more than 1/3, consensus is not reached.
Algo OM(), > 0:
(1) the commander sends his value to every lieutenant
(2) for each , let be the value Lieutenant receives from the commander, or else be RETREAT if he receives no value. Lieutenant acts as the commander in Algo OM( ) to send the value to each of the other lieutenants.
(3) For each , and each , let be the value Lieutenant received from Lieutenant in step (2) (using algo OM()) or else RETREAT if he receives no such value.
Lieutenant uses the majority .
Demo1:
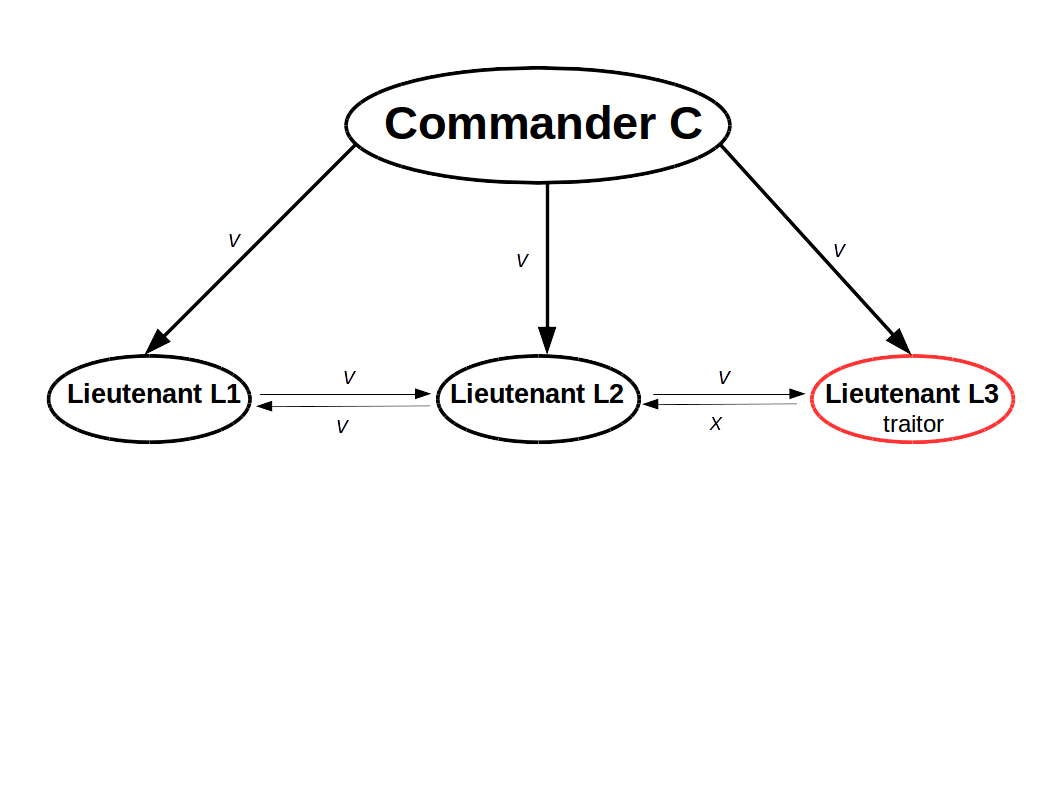
(1) sends to all
| (2) sends to L2 and | L3 sends to |
(3) For for example, values are
The final decision is the majority vote from and as a result consensus has been achieved \
Demo2:
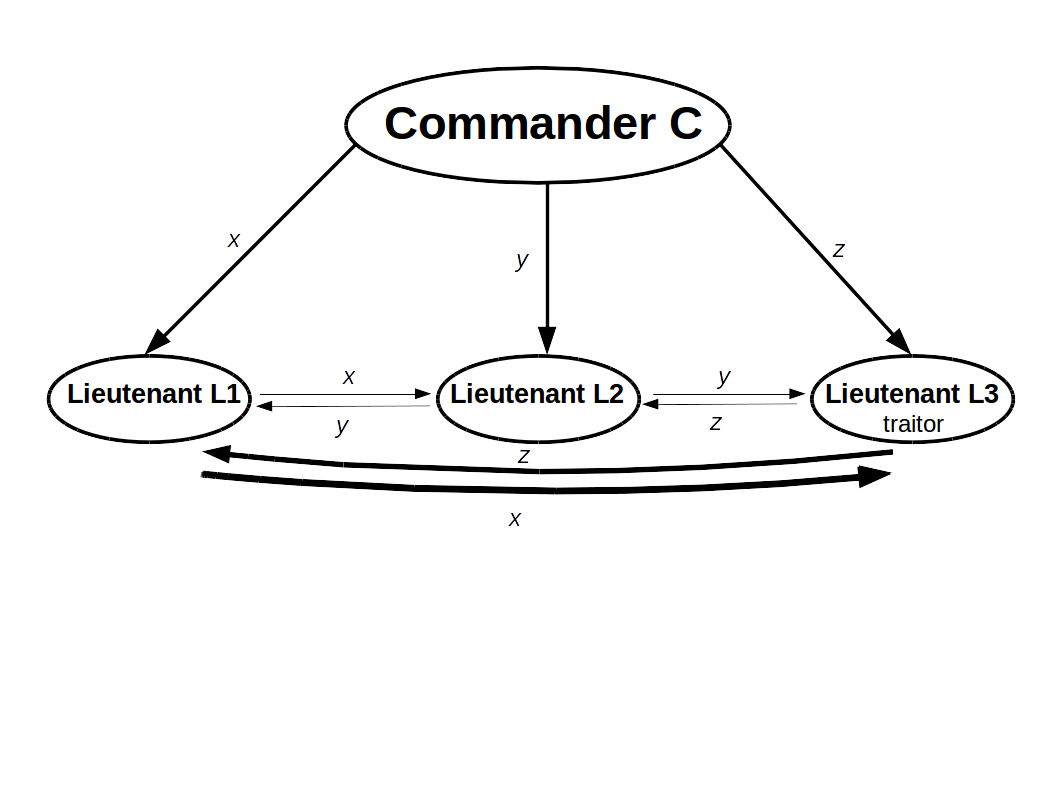
(1) sends to
(2) sends to L2 and L3, and sends to , and sends to
(3) For for example, values are
have all the same value so consensus is reached. are totally different commands, we can assume that they act on the default option retreat.
Byzantine Fault Tolerance
BFT is the characteristic which defines a system that tolerates the class of failures that belong to the Byzantine General’s problem. Byzantine Failure implies no restrictions, makes no assumptions about the kind of behavior a node can have (e.g a node can generate any kind of arbitrary data while posing as an hoinest actor).
BFT is the idea of being certain and everyone else being certain that you all agree on the same thing and if there is disagreement that would be Byzantine Failure.
We say it is Byzantine Fault Tolerant if we can generate cryptographic proof of who the parties are at faults, and then to penalize those parties.
That obliges all parties to cooperate towards a consensus,.
BFT has been needed in any system whose actions depends on the results of a large amount of sensors.
An algo is Byzantine Fault Tolerant as long as the number of traitors does not exceed 1/3 of the generals.
Solutions
Practical Byzantine Fault Tolerance (PBFT)
used by HyperLedger Fabric with pre-selected generals
Pros: efficient / High Transaction throughput Cons: Centralized / Permission
Federated Byzantine Agreement (FBA):
FBA is used by stellar/Ripple.
Generals sort msgs as they come in to establish truth. In Ripple, generals (validators) are pre-selected by Ripple fundation.
Stellar : anyone can be a validator and you choose which validator to trust.
Bitcoin
Bitcoin uses the POW as a probabilistic solution to the Byzantine Gneeral Problems
