https://blog.coast.ai/lets-evolve-a-neural-network-with-a-genetic-algorithm-code-included-8809bece164
http://nn.cs.utexas.edu/downloads/papers/stanley.ec02.pdf
In this post, I detail my implementation of Genetic Algorithm to find the optimum architecture of a Neural Network for classifying image of Dogs and Cats.
Geneticalgorithms are commonly used to generate high-quality solutions optimization and search problems by relying on bio-inspired operators: mutation, crossover and selection. OpenAI published a paper called Evolution Strategies as a Scalable Alternative to Reinforcement Learning where they showed that evolution strategies, while being less data efficient than RL, offer many benefits. The ability to abandon gradient calculation allows such algorithms to be evaluated more efficiently. It is also easy to distribute the computation for an ES algorithm to thousands of machines for parallel computation. By running the algorithm from scratch many times, they also showed that policies discovered using ES tend to be more diverse compared to policies discovered by RL algorithms.
I would like to point out that even for the problem of identifying a machine learning model, such as designing a neural net’s architecture, is one where we cannot directly compute gradients. While RL, Evolution, GA etc., can be applied to search in the space of model architectures, in this post, I will focus only on applying these algorithms to search for parameters of a pre-defined model.

The model is composed of a feature detector, a few blocks of convolutional layers similar to VGG16, and a fully connected classifier with the sigmoid activation function at the output. The model is build with Keras (Tensorflow backend). The Genetic Algorithm is used on the classifier only, and the architecture of the feature detector is unchanged. One additional caveat is that the models are constraint to have less than 500,000 training parameters. The motivation is 2-fold: (1) we narrow down the space search, (2) we can find the best-performing light-weight model suitable for machines with limited ressources such as cellphones, raspberry pi, etc…
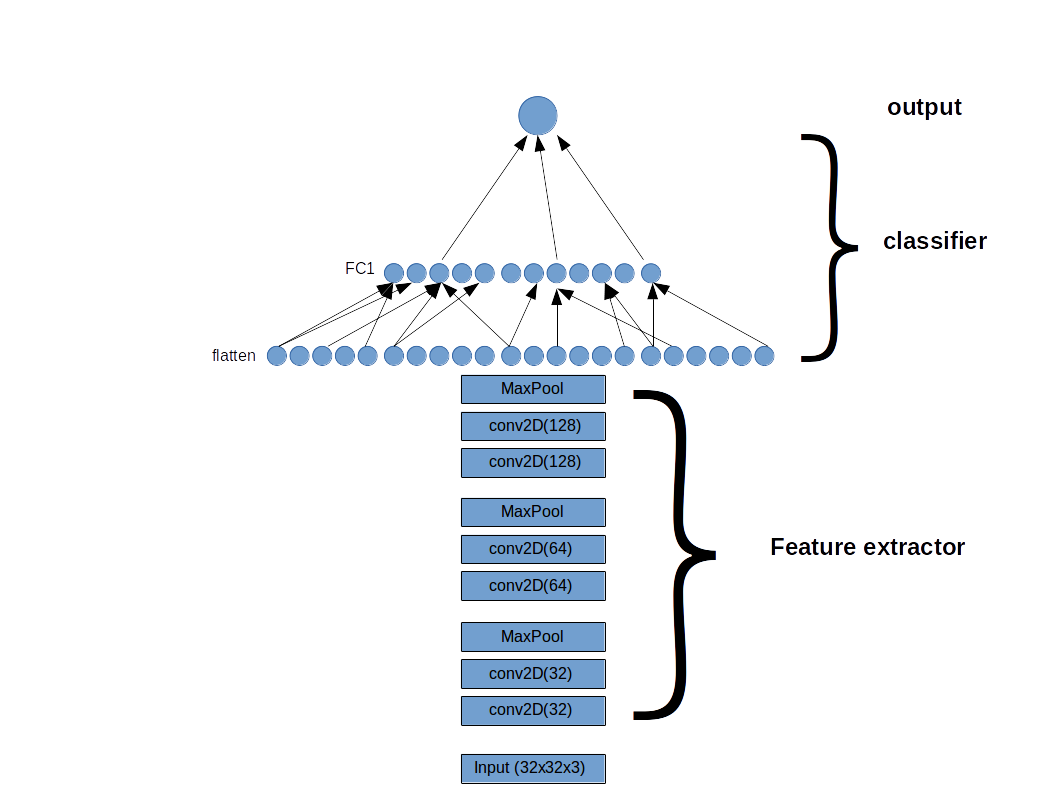
The basic idea is to start with a population of specimens/individuals with random attributes. Through different processes/operators, the specimens are allowed to evolve, i.e the attributes are tuned so to achieve higher performance. The performance of a specimen is evaluated using a fitness function.
For our purpose, the attributes are: the number of hidden layers (from 1 to 10), the number of hidden units (constraint so that the total number of trainable parameters is below 500,000), the activation function (ReLU, eLU, swish), the dropout value (between 0.4 and 1))`. Our choice for the fitness function is the loss of the validation set.
Implementation of the genetic algorithm in 8 steps
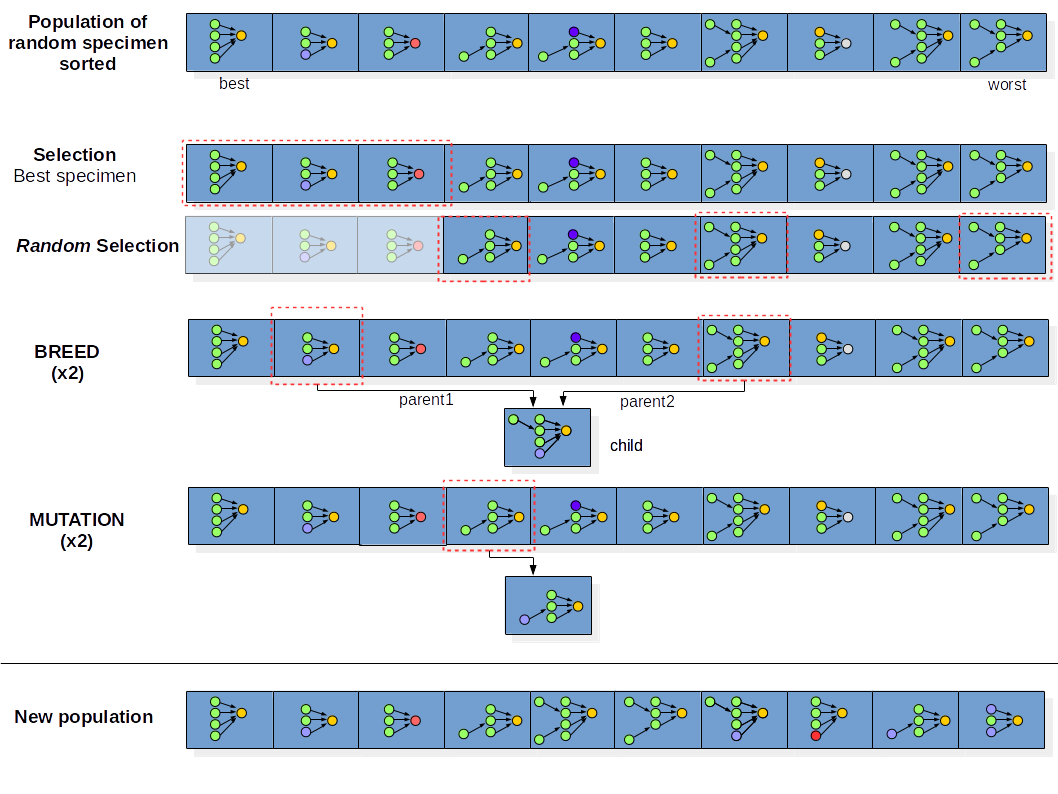
1) Initialization:
We build a population of 20 specimens (ConvNets), where the hyper-parameters and architecture of the classifier are randomly generated
Each specimen is a dictionary of the form:
1
2
3
4
5
6
7
8
9
10
specimen = {
"model": <keras model>,
"classifier_design": [{"units"; 100, "activation": "relu", dropout": 0.5},
{"units"; 30, "activation": "relu", dropout": 0.8},
...
],
"score": 0.34
}
n_population = 20
classifier_design (a list of dict()) gives the architecture of the classifier, i.e the attributes layer-by-layer: units is the number of hidden units in the layer, activation is the non-linear function to be applied , and dropout is the percentage of nodes to keep on during training.
score is the loss of the validation set for the last step of the training.
2) Get the score:
Train all the specimens (ConvNets) using a small subset of the dataset (5000 images) to speedup the training, and record the loss of the validation set
1
2
3
4
5
train_data, validation_data = build_dataset(5000, 0.25)
for idx, specimen in enumerate(population):
specimen["score"], val_acc = train_specimen(train_data, validation_data, specimen["model"], batch_sz=128,
n_epochs=n_epochs, lr=0.0001, patience=patience)
print("score: {} | Accuracy: {}".format(specimen["score"], val_acc) )
3) Sort the specimen by increasing order of the validation loss: The loss is the cross-entropy loss calculate for the validation set:
where $j$ is the sample index. Smaller loss is better.
1
2
def sorted_specimen(self, population):
return sorted(population, key=itemgetter('score'), reverse=False)
4) Select the 5 top specimens:
1
2
3
n_top = 5
def keep_top_specimen(self, n_top, sorted_population):
return sorted_population[0:n_top]
5) Randomly select 5 more specimens from the population:
1
2
3
4
5
n_random_pick = 5
def keep_simple_specimen(self, n_top, n_random_pick, sorted_population):
idx = np.arange(n_top, len(sorted_population))
picks = np.random.choice(idx, n_random_pick)
return [sorted_population[i] for i in picks]
6) Generate 5 ConvNets from breed operator.
Randomly pick 2 specimens (the parents), and decide what attributes to transfer to their child. The attribute to be inherit can be an entire layer or a units, activation or dropout value from one of the parents.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def breed(self, parents):
#index of parent with most hidden layers
deepest_parent = np.argmax( list(map(lambda x: len(x["cls_design"]), parents)))
shallowest_parent = (not( bool(deepest_parent) )) * 1
#Initialize child
child_design = []
for layer_id in range( len(parents[ deepest_parent ]["cls_design"]) -1):
layer = parents[ deepest_parent ]["cls_design"][layer_id]
if layer_id > (len(parents[shallowest_parent]["cls_design"]) - 1):
#shallowest parent does not have this layer level
#==> randomly decide to pick layer of deepest or stop the breed
if np.random.choice([0, 1]):
child_design.append(layer)
break
else:
child_layer = dict()
for key in layer.keys():
pick_gene_from = np.random.choice([deepest_parent, shallowest_parent])
child_layer[key] = parents[pick_gene_from]["cls_design"][layer_id][key]
child_design.append(child_layer)
#append the output layer
child_design.append({"units": 1, "activation": "sigmoid", "dropout": None})
child = {"model": None, "cls_design": child_design, "score": None}
return self.design2model(child)
7) Generate 5 ConvNets from mutate operator:
Randomly pick a specimen from the population and change the value of an attribute: the activation function, the number of units or the value of the dropout. The change in the number of units and dropout can be $+/- 50\%$ of the original value. Note that we clip the lower bound of the number of units to be $\geq 1$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def mutate(self, specimen):
#pick_layer to mutate
pick_layer = np.random.choice( np.arange( 0, len(specimen["cls_design"]) - 2, 1 ) ) #skip the last layer
pick_key = np.random.choice( list( specimen["cls_design"][0].keys() ) )
new_specimen = dict()
new_specimen = specimen["cls_design"]
if pick_key == "units":
range_mutation = [i/10 for i in range(5, 16, 1) if i!=10]
mutation_factor = 1
while mutation_factor == 1:
#insure that the value is changed and allows +/-50% mutation in units
mutation_factor = np.random.choice( range_mutation )
mutation = int(specimen["cls_design"][pick_layer][pick_key] * mutation_factor)
mutation = np.clip( mutation, 1, None ) #units cannot be below 1
new_specimen["cls_design"][pick_layer]["units"] = mutation
#reinitialize model and score for the new specimen
#build and add keras model to the specimen
new_specimen = self.design2model( new_specimen )
return new_specimen
elif pick_key == "dropout":
new_specimen["cls_design"] = specimen["cls_design"]
mutation_factor = 1
range_mutation = [i/10 for i in range(5, 16, 1) if i!=10]
mutation = specimen["cls_design"][pick_layer][pick_key]
while mutation == specimen["cls_design"][pick_layer][pick_key]:
mutation_factor = np.random.choice( range_mutation )
mutation = specimen["cls_design"][pick_layer][pick_key] * mutation_factor
mutation = np.clip( mutation, 0.4, 1 )
new_specimen["cls_design"][pick_layer]["dropout"] = mutation
#build and add keras model to the specimen
new_specimen = self.design2model( new_specimen )
return new_specimen
else:
new_specimen["cls_design"] = specimen["cls_design"]
old_gene = specimen["cls_design"][pick_layer]["activation"]
mutation = old_gene
while mutation == old_gene:
mutation = np.random.choice(self.configs.list_activations())
new_specimen["cls_design"][pick_layer]["activation"] = mutation
#build and add keras model to the specimen
new_specimen = self.design2model( new_specimen )
return new_specimen
8) Build a new population:
The new population is made of the specimens created by the 4 operators: select best, select random, breed and mutate, and has the same size as the previous population.
We then iterate step 2 through step 8 with the new population.
Results
Genetic algorithms help diversity by keeping track of a diverse set of candidate solutions to reproduce the next generation. However, in practice, most of the solutions in the elite surviving population tend to converge to a local optimum over time. There are more sophisticated variations of GA out there, such as CoSyNe, ESP, and NEAT, where the idea is to cluster similar solutions in the population together into different species, to maintain better diversity over time.
One of the most common uses for resistors is to limit the current flowing through an electronic component. Some components, such as light-emitting diodes, are very sensitive to current. A few milliamps of current is enough to make an LED glow; a few hundred milliamps is enough to destroy the LED.
Project 2-1 shows you how to build a simple circuit that demonstrates how a resistor can be used to limit current to an LED.
https://blog.coast.ai/lets-evolve-a-neural-network-with-a-genetic-algorithm-code-included-8809bece164 https://www.youtube.com/watch?v=1i8muvzZkPw https://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol1/hmw/article1.html https://ac.els-cdn.com/S0377042705000774/1-s2.0-S0377042705000774-main.pdf?_tid=073f74ff-3596-4291-901c-898f01cb75fc&acdnat=1523809306_304c126235c248115154b47b62baaefd https://lethain.com/genetic-algorithms-cool-name-damn-simple/ https://blog.coast.ai/lets-evolve-a-neural-network-with-a-genetic-algorithm-code-included-8809bece164
ALTERNATIVE
https://machinelearningmastery.com/grid-search-hyperparameters-deep-learning-models-python-keras/
http://blog.otoro.net/2017/10/29/visual-evolution-strategies/