Search for an element in a sorted array
Example
Let’s consider an array with element values sorted in numerical order (see below)

We want to see if the number [25], we will call it the target value, exists in the array. If we go through the entire array, starting from the first element, it will take O(n) time. A faster approach is detailed below:
1. start in the middle of the array
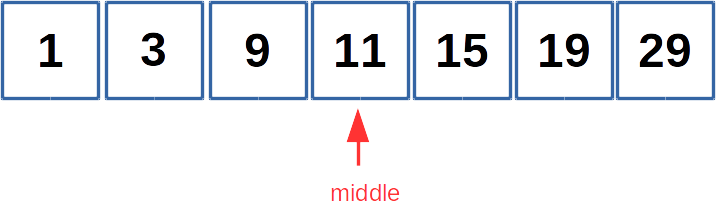
id_mid = (id_end - id_start)//2
2. Check if the number in the middle is smaller or bigger than the target value. If TRUE (smaller), do step 3.
if array[id_mid] == target:
return id_mid
elif array[id_mid] > target:
use top subarray
elif array[id_mid] < target:
use bottom subarray
3. Divide again the 2nd half of the array and find the new middle
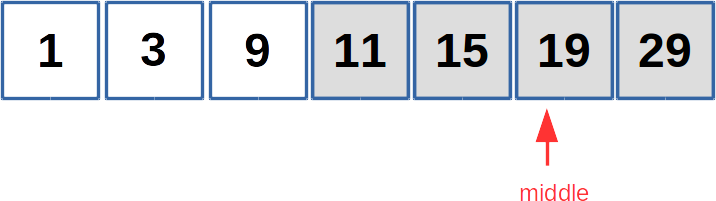
We can reiterate the assumption on the 2nd half of the array.
If the array is not splittable, then always choose the number with lower index.
Binary Search Efficiency
Let’s look at the number of splits/steps for different array size:
* array of 1 element : 1 split
* array of 2 element : 2 splits
* array of 3 element : 2 splits
* array of 4 element : 3 splits
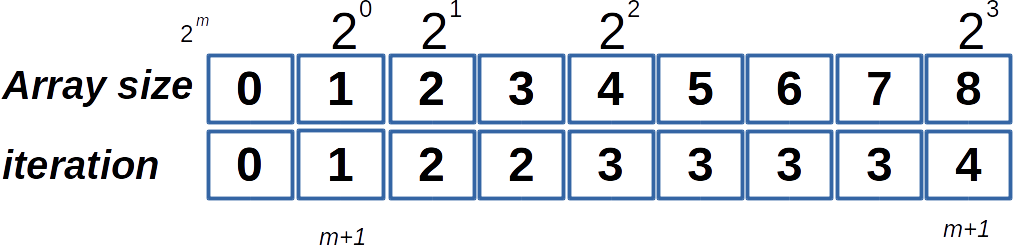
One can see that the number of splits/steps increases when the array length is doubled.
Hence the number of splits scales as
When the array double in size, the number of steps increases by 1, so: O(power of 2 exponent + 1) (
Hence,
We can dismiss the constant 1 and typically is typically .
Python implementation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def binary_search(input_array, value):
if len(input_array) == 0:
return -1
id_start = 0
id_end = len(input_array)
idx = -1
while idx == -1 and id_start <= id_end:
idx_split = (id_start + id_end) // 2
if input_array[idx_split] == value:
idx = idx_split
elif value > input_array[idx_split]:
id_start = idx_split + 1
elif value < input_array[idx_split]:
id_end = idx_split - 1
return idx
test_list = [1,3,9,11,15,19,29]
test_val1 = 25
test_val2 = 15
print(binary_search(test_list, test_val1) )
print(binary_search(test_list, test_val2) )